Gaussian Mixture Model, GMM

왜 Gaussian Mixture Model (GMM)을 기법을 사용할까?

관측한 변수의 분포가 복잡하여 설명이 힘들때 혼합 모델(mixture model)을 사용하여 더 쉽게 설명하기 위해서이다. 이때 보통 잠재 변수(latent variable)를 도입하고, 보통 잠재변수의 분포 모델은 수학적/계산적으로 용이한 모델을 사용한다. 즉, 단순한 모델의 조합으로 복잡한 모델을 설명한다. 결국, 잠재변수의 형태를 사전에 정해야 한다. 예를들면 잠재변수는 gaussian 분포를 따른다고 가정한다. 이러면 Gaussian Mixture Model이 된다.

최종적으로 단순한 모델의 인자들이 추정이 끝이나면, 우리는 복잡한 모델을 잘 설명하는 인자를 추정하게 된 것이다.

잠재 변수($z$)로 복잡한 모델을 설명하기

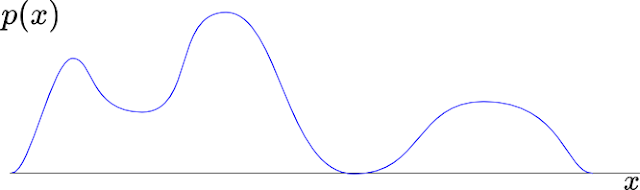
아래의 그림에서 $p(X)$ 분포를 어떻게 모델링해야 하지? 

[그림 1] $p(x)$의 분포

$p(x)$를 보면 특징이 있다. 바로, 봉오리(peak)가 3개가 있다는 것이다($\mu$). 그리고 좌우로 퍼진 정도는 다르다($\sigma$). 그럼 3개의 가우시안 모델을 가지고 설명을 할 수 있다고 생각할 것이다. 그러면 잠재변수($z$)를 3개 놓고, $z$는 가우시안 분포를 따를 것이라 가정하자. 그러면 아래 그림2와 같이 잠재변수의 분포를 가우시안(gaussian) 모델로 그림 1을 설명할 것이다. 물론 오차는 존재한다.

[그림 2] 3개의 잠재변수 $z$로 설명한 $p(x)$ 분포.   여기서, $p(x|z_k)=g(x|\mu_k,\sigma_k)$의 의미는 $z_k$가 주어졌을때의 $x$의 분포이다.

Marginal $x$을 한다는 것은? 잠재변수 $z$의 소거. 그것의 의미는?

단순히 잠재변수를 제거하여 $z$를 고려하지 않겠다는 표현이다. 즉, $z$를 모두 더하여 소거한다. 직관적인 의미를 알아보면 3개의 가우시안 모델이 주어졌을때, 오직 $x$의 관점에서 분포를 알기 위하여 $z$를 선형으로 중첩한 것이다. 결론적으로 잠재변수의 분포 가정과 marginal 연산을 사용하여, 가우시안 모델로 복잡한 $p(x)$를 설명 할 수 있게 된다. 마치 그림 3과같이 3개를 그래프(녹색, 붉은색 그리고 하늘색)를 중첩(표시)해서 핑크색 $p(x)$를 만드는 것과 비슷하다. 이것의 수학적 의미로 잠재변수를 소거를 위한 "marginal한다"는 것과 비슷하다. 물론, 관측된(파란색) $p(x)$와 중첩된(핑크색) $p(x)$사에이는 오차가 있다.

수학의 언어로 모델링 과정을 살펴보자.

잠재변수와 $x$를 수학적 심볼로 해석을 해보자. 우리의 직관을 매우 정교하게 설명한 것뿐이다. 잠재변수($z$)가 있다고 가정하면, 두 변수를 결합한 확률은 단순하게 $$p(x,z) \label{p_x_z}$$ 결합확률 분포로 표현된다. 이것만으로는 $z$로부터 $x$를 표현할 수 없다. 여기서 중첩원리를 이용하자. 바로 marginal이다. 

그러면, $x$의 marginal은 

$$p(x) = \sum_{k=1}^{K} p(x,z_k)$$

가 될 것이다. 하지만, 아직도 $p(x,z_k)$를 우리가 아는 가우시안 모델로 연결을 시키기에는 역부족이다. Factorization기법[참조] 이용해보자. 여기서 $p(x,z_k)$는 $z$로부터 $x$가 생성되는 것을 가정한다면 factorization 원리의 따라서, $p(x,z_k) = p(x|z_k)p(z_k)$가 된다. 

그리므로  $$p(x) = \sum_{k=1}^{K} p(z_k)p(x|z_k) \label{factorization}$$

방정식 $\ref{factorization}$에서 무언가 구체화 됬다($z_k$로부터 $x$를 표현할 수 있다). $p(x|z_k)$는 그림 2에서 한 개의  가우시안 모델로 구체화를 할 수 있다(likelihood이다). Likelihood는 모델의 인자가 정해질 경우 $x$의 확률을 계산할 수 있다. 즉, 그림 2에서의 각 색별로 가우시안 분포를 계산할 수 있다. 수학적으로 자세히 써보면, 가우시안에 근거한 likelihood $p(x|z_k)$는 $N(x|\mu_k,\sigma_k)$가 된다. 잠재변수 $z_k$의 가우시안 모델이라고 할 수 있다.

$p(z_k)$는 $z_k$의 가중치가 된다. 더군다나 $x$와는 상관없는 확률이다. 단순한 더하기의 중첩이 아니라, 가운시안 모델, $p(x|z_k)$의 가중치의 합이다. 

최종적으로 

$$\begin{align}p(x) &=& \sum_{k=1}^{K} p(z_k)N(x|\mu_k,\sigma_k) \nonumber \\ &=& \sum_{k=1}^{K}w(z_k)*N(x|\mu_k,\sigma_k) \label{nzk} \end{align}$$

$p(x,z)$[$\ref{p_x_z}$]의 분포로부터 잠재변수 가우시안 분포[$\ref{nzk}$]까지 구체화를 하였다.

K-Clustering과 GMM의 관계는?

만약 $z_k$가 one-hot encoding일때를 칭한다. One-hot encoding은 1개만 1일고 나머지는 0인 배열을 가지는 것이다. 즉, $z_1$ = [1,0,0], $z_2$ = [0,1,0], $z_3$ = [0,0,1]이 된다. 그리고 K는 여기서 3이다.

그림 2에서 처럼  $x$위에 모든 점들은 likelihood( $p(x|\mu_k,\sigma_k)$ )가 가장 큰 값에 해당하는 색깔을 계산적으로 찾을 수 있다($k=\underset{k}{\operatorname{argmax}} \ {p(x|z_k)}$). 이는 결국 빨강, 녹색과 하늘색 중 하나에 귀속을 판정할 수 있다.

EM을 사용하여 GMM의 인자를 찾는다.

이 모델을 $z_k$를 찾는 방법은 보통 MLE(Maximum Likelihood Estimation)의 해법으로 EM(Expectation Maximization) algorithm을 많이 사용한다.

EM은 보통 2단계로 구성된다:

1. E단계: $(\mu,\sigma)$를 고정하고, 모든 데이터의 $p(z_k|\mu,\sigma)$의 값을 계산한다.
2. M단계: 가장 잘 설명하는 모델의 파라미터($\mu,\sigma$)를 새롭게 갱신한다.
3. 1,2단계 반복, 단, 모델 파라미터의 변화가 작으면 종료한다.

자세한 EM은 다른 글에서 설명하기로 하자.